|
|
|
|
|
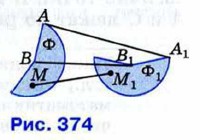
Приложения Об аксиомах планиметрии (продолжение)Чтобы выяснить этот смысл, заметим, что при наложении фигуры Ф на равную ей фигуру Ф1, как мы представляем его наглядно, каждая точка фигуры Ф накладывается на некоторую точку фигуры Ф1. Иначе говоря, каждая точка фигуры Ф сопоставляется некоторой точке фигуры Ф1. Но мы можем сопоставить каждую точку фигуры Ф некоторой точке фигуры Ф1 и без непосредственного наложения Ф на Ф1 (рис. 374). Такое сопоставление называется отображением фигуры Ф на фигуру Ф1 (при этом подразумевается, что каждая точка фигуры Ф1 оказывается сопоставленной некоторой точке фигуры Ф). Под наложением фигуры Ф на фигуру Ф1 мы понимаем отображение Ф на Ф1. Более того, мы считаем, что при этом не только точки фигуры Ф, но и любая точка плоскости отображается на определённую точку плоскости, т. е. наложение — это отображение плоскости на себя.
Однако не всякое отображение плоскости на себя мы называем наложением. Наложения — это такие отображения плоскости на себя, которые обладают свойствами, выраженными в аксиомах (см. ниже аксиомы 7—13). Чтобы сформулировать эти аксиомы, введём понятие равенства фигур. Пусть Ф и Ф1 — две фигуры. Если существует наложение, при котором фигура Ф отображается на фигуру Ф1, то мы говорим, что фигуру Ф можно совместить наложением с фигурой Ф1, или фигура Ф равна фигуре Ф^1. Сформулируем теперь аксиомы о свойствах наложений.
Это означает, что если даны какой-то отрезок АВ и какой-то луч h с началом в точке О, то на луче h существует, и притом только одна, точка С, такая, что отрезок АВ равен отрезку ОС.
Это означает, что если даны какой-то луч ОА и какой-то неразвёрнутый угол CDE, то в каждой из двух полуплоскостей с границей ОА существует, и притом только один, луч ОВ, такой, что угол CDE равен углу АОВ.
Как видно, все приведённые аксиомы соответствуют нашим наглядным представлениям о наложении и равенстве фигур и поэтому не вызывают сомнений. Следующие две аксиомы связаны с измерением отрезков. Прежде чем их сформулировать, напомним, как измеряются отрезки. Пусть АВ — измеряемый отрезок, PQ — выбранная единица измерения отрезков. На луче АВ отложим отрезок АА1 = PQ, на луче A1B — отрезок A1A2 = PQ и т. д. до тех пор, пока точка Аn не совпадёт с точкой В либо точка В не окажется лежащей между Аn и Аn + 1. В первом случае говорят, что длина отрезка АВ при единице измерения PQ выражается числом n (или что отрезок PQ укладывается в отрезке АВ n раз). Во втором случае можно сказать, что длина отрезка АВ при единице измерения PQ приближённо выражается числом n. Для более точного измерения отрезок PQ делят на равные части, обычно на 10 равных частей, и с помощью одной из этих частей измеряют описанным способом остаток АnВ. Если при этом десятая часть отрезка PQ не укладывается целое число раз в измеряемом остатке, то её также делят на 10 равных частей и продолжают процесс измерения. Мы предполагаем, что таким способом можно измерить любой отрезок, т. е. выразить его длину при данной единице измерения конечной или бесконечной десятичной дробью. Это утверждение кратко сформулируем так:
|
|
|